弹性
量化某个变量随着另一个变量的变化而变化的程度
- 弹性大:因变量对自变量的变化很敏感
- 弹性小:因变量对自变量的变化不怎么敏感
Price Elasticity of Demand
量化
PED=percentage change in Pricepercentage change in Quantity demanded=%ΔP%ΔQd
两点 PED 计算公式
我们用中点代为计算 Percentage Change
Percentage=(New+Old)/2New−Old那么 PED 的计算公式可以改写成
PED=Pnew−PoldQnewd−Qoldd×Qnewd+QolddPnew+Pold当某个点 old 已经被固定了的时候,考虑其差值 ΔQ→0,就有
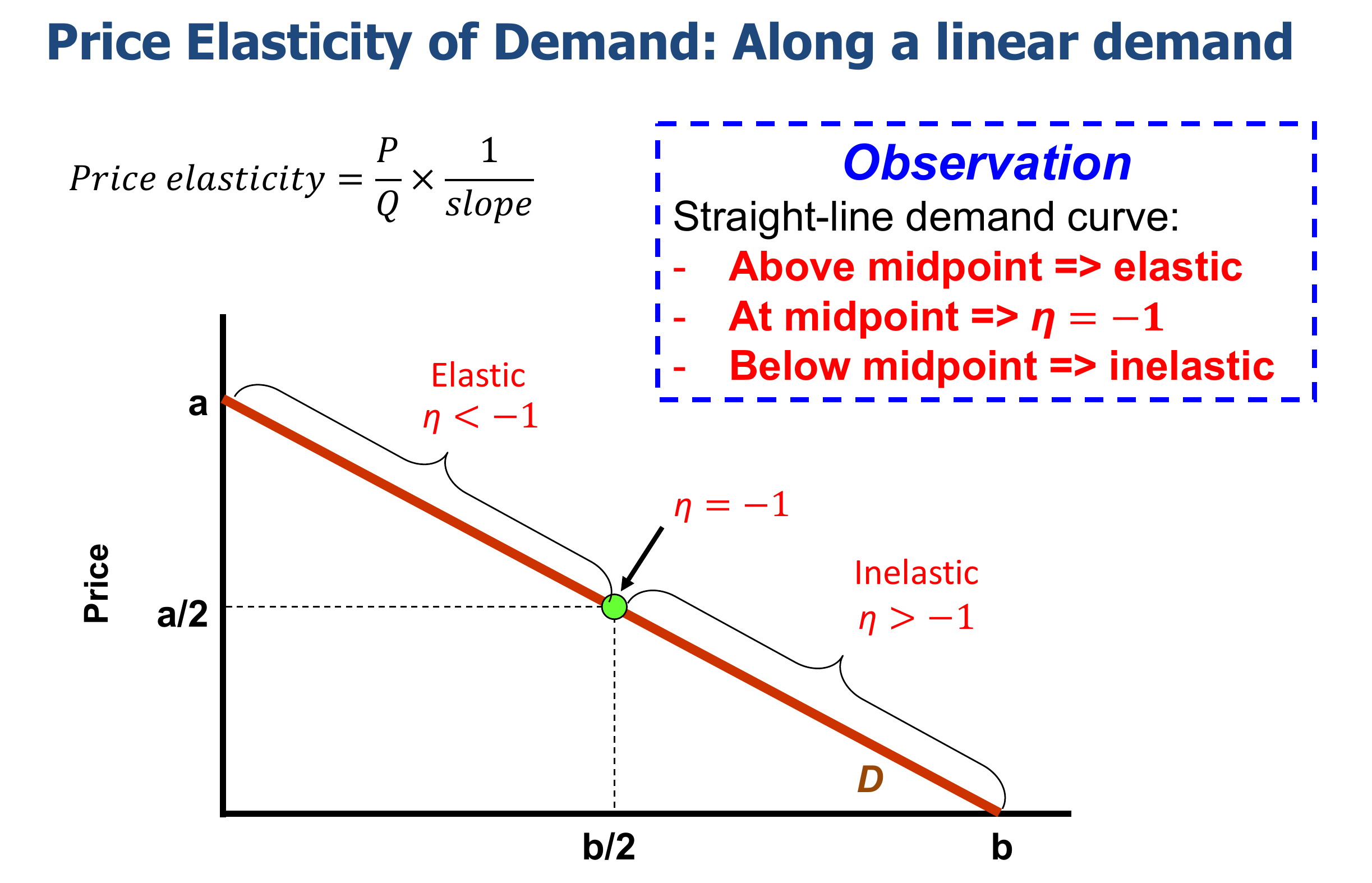
PED=ΔPΔQd×2Qoldd+ΔQd2Pold+ΔP→ΔPΔQd×QolddPold→QdP×slope1 Observation
Price Elasticity 随着点在 Quantity of Demand 曲线上的移动而变化;并且在中点处为 −1,往上 <−1,往下 >−1

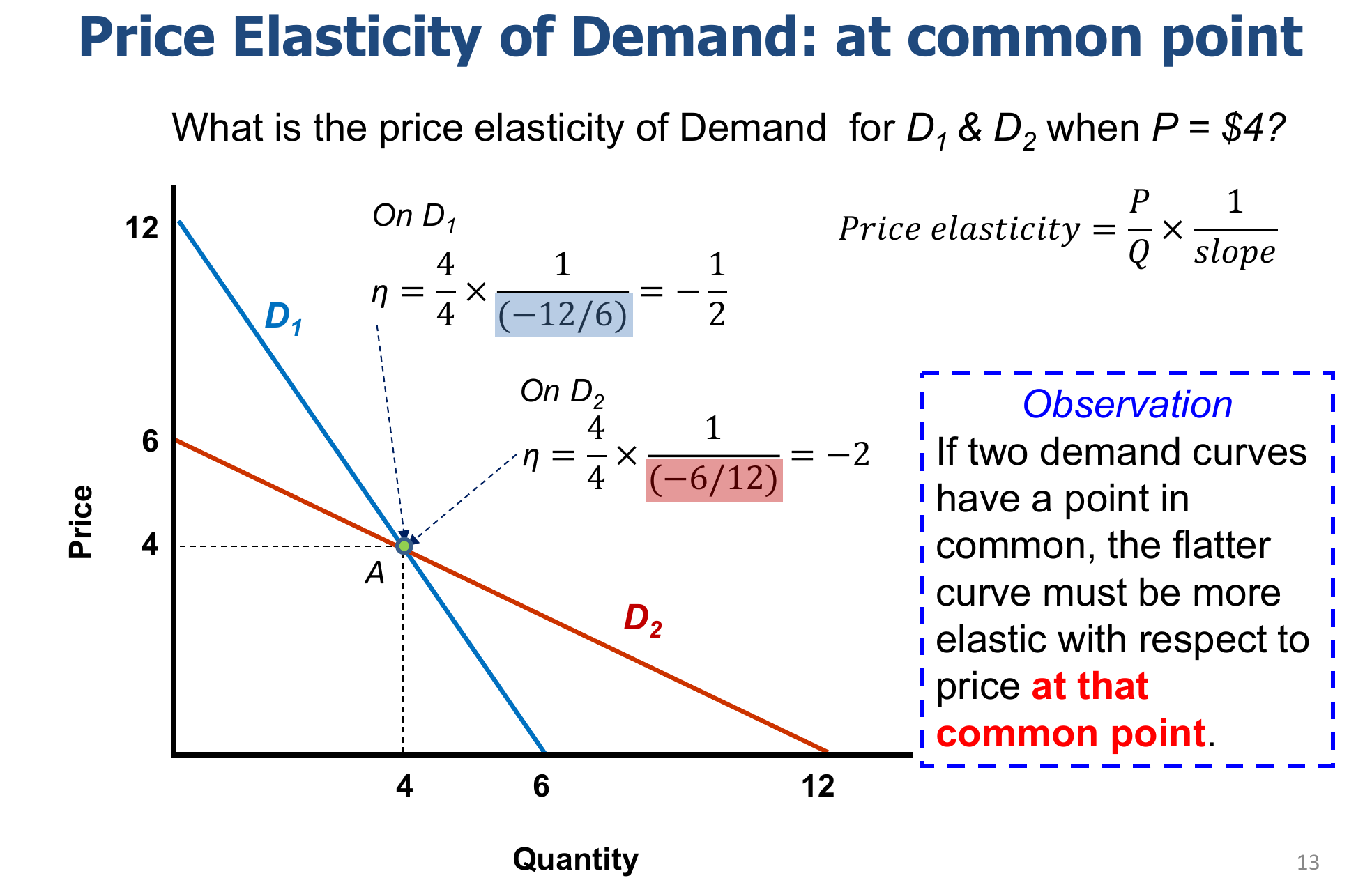
如果两条 Qd 曲线有交点,那么更加平缓的那条直线在这个点上的弹性更大。

Elasticity 与 Revenue
收入基本公式
Revenue=Quantity×Price因此考虑 Elasticity 的话,Revenue 是关于 Price 的二次函数,并且在 PED=−1 的时候,取到最大值
- 弹性需求(∣η∣>1):降价增加总收益(需求量增幅 > 价格降幅)。
- 非弹性需求(∣η∣<1):降价减少总收益(需求量增幅 < 价格降幅)。
- 单位弹性(∣η∣=1):总收益最大。
也可以在 Qd 直线上直观地进行比较:找到点变化前后对应的矩形变化面积。更一般的,如果点在中点上方,则总收益一定增加;在下方则总收益减少。
Constant Elasticity
如果一条曲线在每一个点的 P Elasticity of Q 都相等为 −k,那么其曲线可以表示为
f(P,Q):PkQ=C
证明(不考)
考虑 Q-P 曲线 f 在这一个点的 Elasticity,用点斜式即为
Elasticity=−k=QP×dPdQ把 xdx 放到一起:
−PkdP=Q1dQ两边积分
−klnP+CPlnQ+klnPPkQ=lnQ+CQ=c=C
左右取对数,曲线方程也可以写作
lnQ=−klnP+c 影响 Price Elasticity of Demand 的因素
- Availability of Substitutes
- Time Horizon 产品有效期
- Category of product (specific or broad)
- Necessities vs. Luxuries
- Purchase Size
Substitutes
- Fewer substitutes makes it harder for consumers to adjust Q when P changes… so demand is more inelastic.
- Many substitutes? Switching brands when prices change is easy, so demand is more elastic.
Time Horizon
Category
另外两种 Elasticity
Cross-Elasticity
Exy=%ΔP of Y%ΔQd of X=QxdPy×ΔPyΔQxExy>0 说明是 Substitute ;反之,说明是 complement
Income Elasticity
EI=%ΔIncome%ΔQd=QxI×ΔIΔQx
- EI>1 说明是 Luxury
- EI>0 说明是 Normal Goods
- EI<0 为 Inferior Goods
Price Elasticity of Supply
类似的,也有中点公式和点斜公式
性质
- PES>0
- 若截距 >0,那么随着 Qs 增加,PES 降低,但永远 >1
- 若过原点,则 PES≡1
影响因素
Change in Per-Unit Costs with Increased Production
Time Horizon
Share of Market for Inputs
Geographic Scope
Elasticity and Quick Predictions
把基准点放在 Equilibrium Point,记 ηs 为 Price Elasticity of Supply,ηd 为 Price Elasticity of Demand,则有
% change in Price from a shift in Demand ΔQd=ηs+∣ηd∣% change in Demand ΔQd% change in Price from a shift in Supply ΔQs=−ηs+∣ηd∣% change in Supply ΔQs
例题
2024 Summer
Suppose there is only an initial shift of demand or supply (but not both), and we observe that the equilibrium price of computers increases by 2.1%, and the equilibrium quantity increases by 8.1%, we conclude that:
A) The price elasticity of demand is elastic.
B) The price elasticity of demand is inelastic.
C) The price elasticity of supply is elastic.
D) The price elasticity of supply is inelastic.
解答
Price 和 Quantity 都上涨了,因此这一定是 Demand 增加引起的 (Demand Curve right shift)。
上涨的幅度由 Supply Curve 的斜率决定,这里 %ΔP=2.1%,%ΔQ=8.1%,所以 price elasitcity of supply 等于
Es=%ΔP%ΔQ>1由此,price elasticity of supply 是 elastic 的。