Representation

图像生成模型的本质是一个概率模型：如果我们知道了真实图像 xx 的分布规律 p(x)p(x)，那么我们只需要从这个分布里随便采样 x′∼p(x)x'\sim p(x)，那么 x′x' 就是我们想要生成的图像。

不过通常，p(x)p(x) 很难表示和学习。我们考虑通过两个步骤生成图像：

  1. 先生成图片的特征，例如想要生成二次元图片，就先指定 tags 例如发色、动作等等
  2. 在根据特征，去生成图像

我们用 zz 表示图像的“特征” (latent variable)，那么这样的过程就是如同下面所示

z⟶guidex \boxed{z}\overset{\text{guide}}{\longrightarrow} \boxed{x}

用数学语言描述就是这样一个恒等式

p(x)=∑zp(x∣z)⋅p(z) p(x)=\sum_z p(x|z)\cdot p(z)

VAE 的推理从数学的角度也就变成了

  1. Sample zz from p(z)p(z)
  2. Sample xx from p(x∣z)p(x|z)

当然，由于我们的目的是简化 p(x)p(x) 的建模，因此我们通常假设

p(z)∼N(0,1)p(x∣z)∼N(μθ(z),Σθ(z)) \begin{aligned} p(z)&\sim \mathcal N(0,1)\\ p(x|z)&\sim \mathcal N(\mu_\theta(z),\Sigma_\theta(z)) \end{aligned}

其中 μθ(⋅),Σθ(⋅)\mu_\theta(\cdot),\Sigma_\theta(\cdot) 是神经网络。

这里也不一定非得是正态分布，其他容易计算的分布也可以。简单起见直接用正态分布了

Inference

Inferencing Objective Function

给定一个数据集 D={x1,x2,…,xm}\mathcal D=\{x^{1}, x^{2}, \dots, x^{m}\}，模型训练目标就是，从数据集 D\mathcal D 里训练的图像分布 pθ(x)p_\theta(x) 和真实的图像分布 p(x)p(x) 尽可能接近。衡量两个分布接近程度可以用 KL 散度，即训练目标为最小化 KL 散度：

min⁡θDKL(pθ(x)∥p(x)) \min_\theta D_{KL}\Big( p_\theta(x) \big\| p(x) \Big)

最小化 KL 散度等同于最大化 Marginal Log-Likelilhood log⁡pθ(x)\log p_\theta(x) over D\mathcal D

max⁡θ∑xi∈Dlog⁡pθ(xi)=max⁡θ∑xi∈Dlog⁡(∑zpθ(xi,z)) \begin{aligned} &\max_\theta \sum_{x^{i} \in\mathcal D} \log p_\theta(x^{i})\\ =&\max_\theta \sum_{x^{i} \in\mathcal D} \log \Big(\sum_z p_\theta(x^{i},z)\Big) \end{aligned}

然而，zz 是高维空间的隐变量，∑z\sum_z 需要遍历所有可能的 zz、计算 pθ(xi,z)p_\theta(x^{i},z)、再相加，几乎是不可能做到的，我们只能用各种方法去近似求解 log-likelihood

via Monte Carlo

我们随机采样一些 zi∼p(z)z^{i} \sim p(z)，用这些采样的 ziz^{i} 计算平均值：

log⁡pθ(x)≈log⁡1k∑i=1kp(x∣zi),zi∼p(z) \log p_\theta(x)\approx \log \frac{1}{k}\sum_{i=1}^k p(x|z^{i}), \quad z^{i}\sim p(z)

尽管理论上，蒙特卡洛估计方法是 no-bias 的，但是在实战中，用蒙特卡洛计算出来的梯度具有很大的方差。

via Importance Sampling

比起直接 maximize 目标，我们也可以构造出目标的 lower bound 然后通过 maximize 这个 lower bound 从而 maximize 目标。

此处，log⁡pθ(x)\log p_\theta(x) 的一个下界被称为 ELBO (Evidence Lower Bound)

pθ(x)=∑zq(z)q(z)pθ(x,z)=∑zq(z)⋅pθ(x,z)q(z)=Ez∼q(z)[pθ(x,z)q(z)]log⁡pθ(x)=log⁡Ez∼q(z)[pθ(x,z)q(z)]=log⁡∑zq(z)⋅pθ(x,z)q(z)≥∑zq(z)⋅log⁡pθ(x,z)q(z)‾by Jensen’s Inequality=Ez∼q(z)[log⁡pθ(x,z)q(z)]≔ELBO(x;θ)=Lθ(x) \begin{aligned} p_\theta(x) &=\sum_z \frac{q(z)}{q(z)}p_\theta(x,z)\\ &=\sum_z q(z)\cdot \frac{p_\theta(x,z)}{q(z)}\\ &=\mathbb E_{z\sim q(z)}\Big[\frac{p_\theta(x,z)}{q(z)}\Big]\\ \log p_\theta(x)&=\log \mathbb E_{z\sim q(z)}\Big[ \frac{p_\theta(x,z)}{q(z)} \Big]\\ &= \log \sum_z q(z)\cdot \frac{p_\theta(x,z)}{q(z)}\\ &\ge \underset{\scriptsize\text{by Jensen's Inequality}}{\underline{\sum_z q(z)\cdot \log\frac{p_\theta(x,z)}{q(z)}}}\\ &=\mathbb E_{z\sim q(z)}\Big[ \log\frac{p_\theta(x,z)}{q(z)} \Big]\\ &\coloneqq \text{ELBO}(x;\theta)=\mathcal L_{\theta}(x) \end{aligned}
从 KL 散度的视角理解 ELBO

而实际上

log⁡pθ(x)=Ez∼q(z)[log⁡pθ(x,z)]+H(q)entropy of q(z)‾ \log p_\theta(x)=\mathbb E_{z\sim q(z)}\Big[ \log p_\theta(x,z) \Big] + \underset{\overline{\scriptsize\text{entropy of }q(z)}}{H(q)}

直觉上理解，我们选取的 q(z)q(z) 应该同模型从图像出发对特征的预测接近，即

DKL(q(z)∥pθ(z∣x)) D_{KL}\Big( q(z) \big\| p_\theta(z|x) \Big)

越小越好。而 DKL()D_{KL}() 具有非负性，移项后便是 ELBO 的形式。一般形式的，也有

log⁡pθ(x)=ELBO+DKL(q(z)∥pθ(z∣x)) \log p_\theta(x)=\text{ELBO}+D_{KL}\Big( q(z)\big\|p_\theta(z|x) \Big)

然后我们就又可以用 Monte Carlo 方法估计 ELBO 了。

ELBO(x;θ)≈1k∑i=1klog⁡pθ(x,zi)q(zi),zi∼q(z) \text{ELBO}(x;\theta)\approx \frac{1}{k}\sum_{i=1}^k \log\frac{p_\theta(x,z^{i})}{q(z^{i})},\quad z^{i}\sim q(z)

VAE: Decoder 与 Encoder

from Decoder to Encoder: Variational Inference

到目前位置，我们实际上只讨论了 Decoder 部分：pθ(x∣z)p_\theta(x|z)。为了训练模型，我们肯定还需要 x→zx\to z 的推理与训练。这就是 VAE 里 Encoder 的作用。

Encoder 负责的就是 pθ(z∣x)p_\theta(z|x)，但是 pθ(z∣x)p_\theta(z|x) 很难从神经网络模型中推导出来。不过，根据上文对 ELBO 与 KL 散度 DKL(q(z)∥pθ(z∣x))D_{KL}\Big( q(z)\big\| p_\theta(z|x) \Big) 的分析，我们其实也可以通过优化 q(z)q(z) 让其近似 pθ(z∣x)p_\theta(z|x) 来达成相同的目的。

所以，我们把 q(z)q(z) 也用神经网络建模为 qϕ(z)q_\phi(z)，其中 ϕ\phi 为 Encoder 模型的参数，此时 ELBO 改写为

ELBO=Lθ,ϕ(x)=∑zqϕ(z)log⁡pθ(z,x)+H(qϕ(z)) \text{ELBO}=\mathcal L_{\theta,\phi}(x)=\sum_z q_\phi(z)\log p_\theta(z,x)+H(q_\phi(z))

Amortized Inference

注意：这里的 Decoder 与 Encoder 本质上是对分布进行建模，即给定张量，输出一个分布。

如果 Encoder 部分我们为每一个输入的图像都训练一个 Encoder qϕ(z)q_\phi(z)，计算代价无法承受。

因此，我们用神经网络对分布进行拟合，即 gλ:xi↦qϕi(z)g_\lambda:x^{i} \mapsto q_{\phi^{i}}(z)，这样就可以避免反复求解 ϕi\phi^{i} 了。

而对 Decoder 部分就不用了，因为 pθ(x∣z)p_\theta(x|z) 的 zz 是由 Encoder 完成的，而每一个而 Encoder 总是输出的 qϕ(z)≈pθ(z∣x)q_\phi(z)\approx p_\theta(z|x) 总是映射到同一个 random variable space 里.

Training

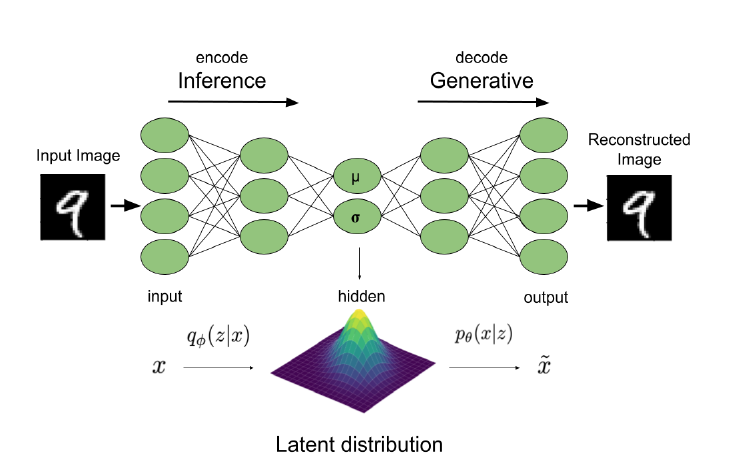
VAE 有一个 Encoder 架构，负责将图像 xx 编码为 latent variable zz；Decoder 架构则负责从 latent variable zz 生成出图像 xx.

VAE
VAE

上文的 ELBO 则为我们优化 VAE 模型提供了一个良好的目标函数：（其实应该是求解上文的 λ\lambda）

max⁡θ,ϕELBO=max⁡θ∑x∈Dmax⁡ϕEqϕ(z)[log⁡pθ(z,x)qϕ(z)]⇒max⁡θ,λ∑x∈Dmax⁡λEgλ(x)[log⁡pθ(z,x)gλ(x)] \begin{aligned} \max_{\theta,\phi}\text{ELBO}&=\max_{\theta}\sum_{x\in\mathcal D}\max_{\phi}\mathbb E_{q_\phi(z)}\Bigg[ \log\frac{p_\theta(z,x)}{q_\phi(z)} \Bigg]\\ &\Rightarrow\max_{\theta,\lambda}\sum_{x\in\mathcal D}\max_\lambda\mathbb E_{g_\lambda(x)}\Bigg[ \log\frac{p_\theta(z,x)}{g_\lambda(x)} \Bigg] \end{aligned}

Stochastic Variational Inference

用随机梯度下降法进行学习

  1. 初始化 θ,ϕ1…m\theta,\phi^{1\dots m}
  2. 随机一个 xi∈Dx^{i} \in\mathcal D
  3. 先优化 ϕi\phi^{i}：
    1. ϕi←ϕi+η∇ϕiLθ,ϕ(xi)\phi^{i}\gets \phi^{i}+\eta \nabla_{\phi^{i}}\mathcal L_{\theta,\phi}(x^{i})
    2. 直到收敛为止
  4. 更新 θ\theta：θ←θ+η∇θLθ,ϕi(xi)\theta\gets\theta+\eta\nabla_{\theta}\mathcal L_{\theta,\phi^{i}}(x^{i})。回到 step 2 继续执行。

那么我们如何计算梯度呢？因为很有可能这个式子并不存在 closed form，我们依然采用 Monte Carlo 的方法解决问题，即

Eqϕ(z)[log⁡pθ(z,x)−log⁡qϕ(z)]≈1K∑i=1Klog⁡pθ(zi,x)−log⁡qϕ(zi) \mathbb E_{q_\phi(z)}\Bigg[ \log p_\theta(z,x)-\log q_\phi(z) \Bigg]\approx \frac{1}{K}\sum_{i=1}^{K}\log p_\theta(z^{i},x)-\log q_\phi(z^{i})

其中 qϕ(z)q_\phi(z) 应该容易采样和计算。由此，ELBO 关于 θ\theta 的导数即为

∇θEqϕ(z)[log⁡pθ(z,x)−log⁡qϕ(z)]≈1K∑i=1K∇θlog⁡pθ(zi,x) \nabla_\theta \mathbb E_{q_\phi(z)}\Bigg[ \log p_\theta(z,x)-\log q_\phi(z) \Bigg]\approx \frac{1}{K}\sum_{i=1}^K \nabla_\theta \log p_\theta(z^{i},x)

然而 ELBO 关于 ϕi\phi^i 的导数不那么好算，因为期望本身依赖于这个参数。一般而言，可以使用强化学习的方法进行学习，也可以使用 Reparameterization 的方法。

Reparam

我们把 qϕ(z)∼N(μ,σ2I)q_\phi(z)\sim \mathcal N(\mu, \sigma^2 I)，即 ϕi=(μ,σ)\phi^i=(\mu,\sigma)，那么从这个正态分布采样就等同于

ϵ∼N(0,1)z=μ+σϵ=gϕ(ϵ) \epsilon\sim \mathcal N(0,1)\\ z=\mu+\sigma\epsilon=g_\phi(\epsilon)

借用这个想法，我们可以改写 ELBO，这里先让 r(z)=log⁡qϕ(z)r(z)=\log q_\phi(z) 简化计算，稍后再代入

Ez∼qϕ(z)[r(z)]=∑zqϕ(z)r(z)=Eϵ∼N(0,1)[r(gϕ(ϵ))]=∫N(ϵ)r(μ+σϵ)dϵ∇ϕEqϕ(z)[r(z)]=∇ϕEϵ[r(gϕ(ϵ))]=Eϵ[∇ϕr(gϕ(ϵ))]≈1K∑i=1Kr(gϕ(ϵi))‾Monte Carlo Estim \begin{aligned} \mathbb E_{z\sim q_\phi(z)}[r(z)]&=\sum_z q_\phi(z)r(z)\\ &=\mathbb E_{\epsilon\sim\mathcal N(0,1)}[r(g_\phi(\epsilon))]\\ &=\int \mathcal N(\epsilon) r(\mu+\sigma\epsilon) d\epsilon\\ \nabla_\phi \mathbb E_{q_\phi(z)}[r(z)]&=\nabla_\phi \mathbb E_\epsilon [r(g_\phi(\epsilon))]\\ &=\mathbb E_{\epsilon}[\nabla_\phi r(g_\phi(\epsilon))]\\ &\approx \underset{\text{Monte Carlo Estim}}{\underline{\frac{1}{K}\sum_{i=1}^K r(g_\phi(\epsilon^i))}} \end{aligned}