回文树

回文树

回文树基于三个重要的观察：

代码实现

回文树的构建

回文树依赖若干个数据结构

1. 树上的每一个节点实际上代表了一个以 $i$ 为结尾的最长回文串（从根到 $s[i]$）
2. 对于树上的实边 next[] 指针，next[i]["c"] = j 说明在以 $i$ 为结尾的最长回文串的两边各添加字符 "c"（其实也就是 $s[j]$）之后，就变成了以 $j$ 为结尾的最长回文串。
3. 对于树上的虚边 fail[] 指针，它实际上维护的是以 $i$ 为结尾的次长回文串。如果 fail[i] = j，则次长的回文串是 node[j]，其中 node[j] 表示树上节点 $j$ 代表的最长回文串
   • 没错，也就是说此时以 $i$ 为结尾的次长回文串和以 $j$ 为结尾的最长回文串是一样的。但是我们又必须以 $i$ 为结尾，所以我们只需要知道其长度信息即可。

要注意的是，节点建模的是“回文串”而不是“以 $i$ 为结尾的最长回文串”，因为以 $i$ 为结尾可能有很多回文串，我们就是要通过 fail 指针快速查找以 $i$ 为结尾的回文串的长度，所以回文串以 $i$ 结尾还是 $j$ 结尾（对于长度这个信息而言）无关紧要。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

using indexing  = int;
constexpr int N = 5e5 + 5;
constexpr int E = 26;
struct Node {
    std::array<indexing, E> next; // 实边
    indexing fail{0}; // 虚边 fail 指针

    int len{0}; // 这个节点对应的回文串 的长度
    int num{0}; // 多少回文串以 节点i代表的最长回文串最末尾的字符 为结尾
    int count{0}; // 这个节点对应的回文串 的数量
    void init(int len) {
        this->len   = len;
        this->count = 0;
        fail        = 0;
        next.fill(0);
    }
};
std::array<Node, N> T;
std::array<int, N> S;
indexing last = 0, pnode = -1, strend = -1;

// 构造一个新节点，放在末尾
indexing construct(int len) {
    T.at(++pnode).init(len);
    return pnode;
}

// 初始化，添加偶根和奇根节点
// 在最开头插入一个不可能出现的字符，减少后面的特判
void init() {
    // 0: 偶根，1: 奇根
    construct(0), construct(-1);
    T[0].fail = 1;
    S[++strend] = -1;
    last = 0;
}

跳 fail 指针

然后我们先来看如何跳 fail 指针。跳 fail 指针的核心在于，对于当前字符 $S[i]$ 找到一个位置 $j$ 使得 $S[i]=S[j]$。

如果指针当前指向的 $v$、其代表的回文串为 $p(v)$，则 $j=i-p(v).\texttt{len}-1$。如果无法匹配，我们就跳 fail 指针 $j\gets j.\texttt{fail}$，即我在满足 $S[j\dots i-1]$ 是回文串的条件下缩小这个后缀回文串的长度，然后判断 $i$ 能组成的后缀回文串的最大长度。

1
2
3
4
5
6
7

// 返回 pos 使得
// T[pos].len 最大，且 S[strend - T[pos].len - 1] ~ S[strend] 构成回文串
indexing match(indexing pos) {
    while (S[strend] != S[strend - T[pos].len - 1]) 
        pos = T[pos].fail;
    return pos;
}

在字符串末尾插入字符

然后我们执行插入字符操作。我们需要做两件事：

1. 维护 next[] 指针（实边）
2. 维护 fail 指针（虚边）

对于实边而言，我们找到一个第一个 pos 使得 S[i-T[pos].len-1] ~ S[i] 构成回文串，那么根据定义，$i$ 应该成为 pos 的儿子节点，边权为 S[i].

对于虚边而言，我们需要找到下一个 $j$ 使得

既然 $S[j\dots i]$ 是回文串，那么 $S[j+1\dots i-1]$ 也应该是回文串，且 $S[j]=S[i]$。这不就是要找 $S[i-1]$ 为结尾的回文串嘛！不过由于是 fail 指针，所以这里的“回文串”其实不是指最长回文串，也就是说，我们需要从 pos.fail 开始跳 fail 指针，以免用最长回文串来更新 fail.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

void insert(int c) {
    S[++strend] = c;
    indexing fa = match(last);
    indexing son = T[fa].next[c];
    if (!son) {
        son = construct(T[fa].len + 2);
        T[son].fail = T[match(T[fa].fail)].next[c];
        T[fa].next[c] = son;
        T[son].num = T[T[son].fail].num + 1;
        // 注意这里必须先维护 fail 再更新子节点
        // 不然可能出现当 fa 为偶根和奇根的时候 T[son].fail = son
    }
    last = son;
    T[son].count++;
}

在字符串的开头插入字符

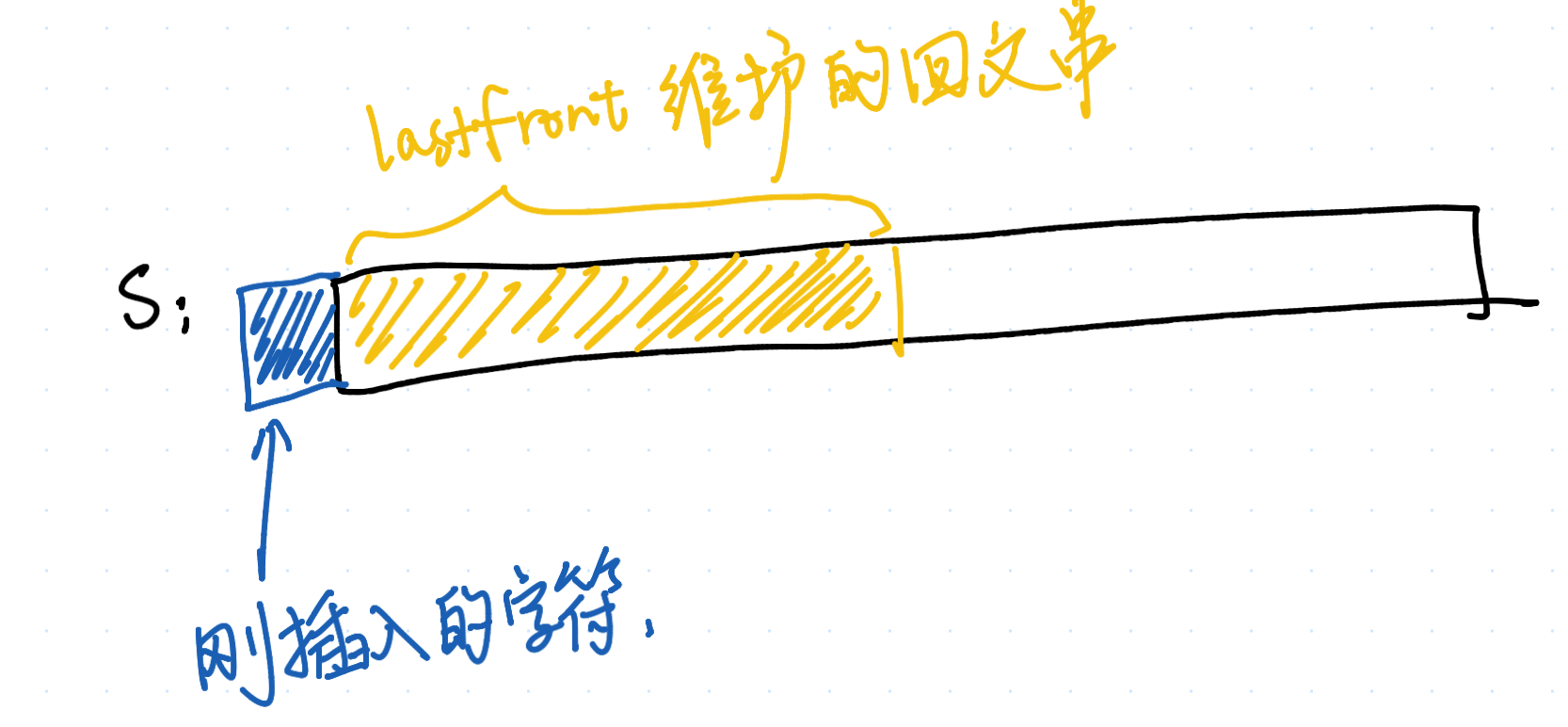
在末尾插入比较好理解，考虑当前在维护第 $i$ 个字符，last 刚好可以代表以 $S[i-1]$ 为结尾的最长回文串。那如果需要在字符串开头插入字符呢？

类似的，我们想，是不是需要用 last_front 表示以 $S[0]$ 为开头的最长回文串，然后跳 fail 呢？但是我们的节点维护的都是以某个字符为结尾的回文串，应该怎么转化呢？

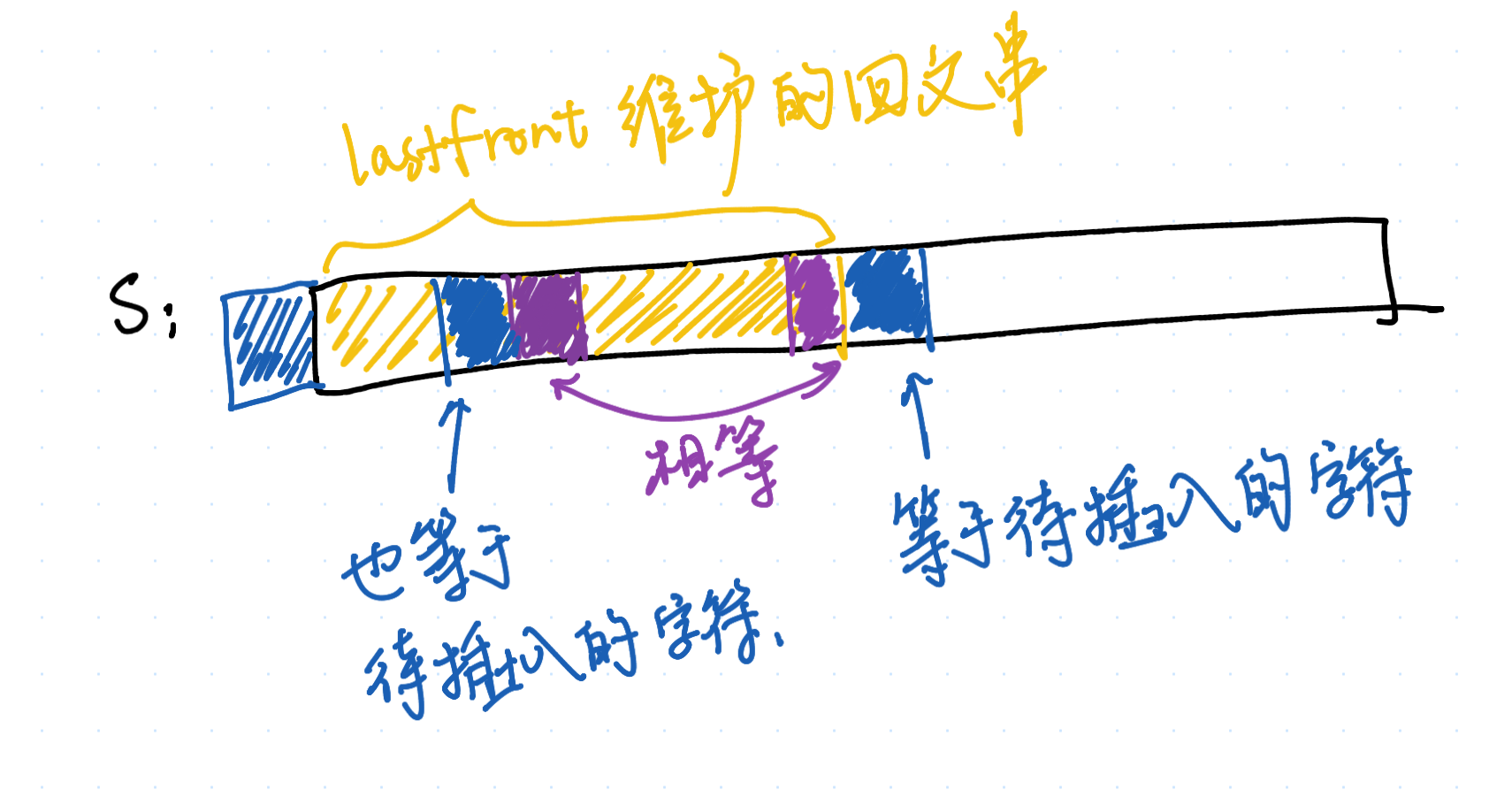
这里，我们就需要以“节点对应的是回文串”视角来看待 last 和 last_front 指针了（而非“节点对应的是以 $i-1$ 为结尾的回文串”）。last_front 指针保存的回文串，是从 S.front() 为开头的最长回文串。

last_front 指针

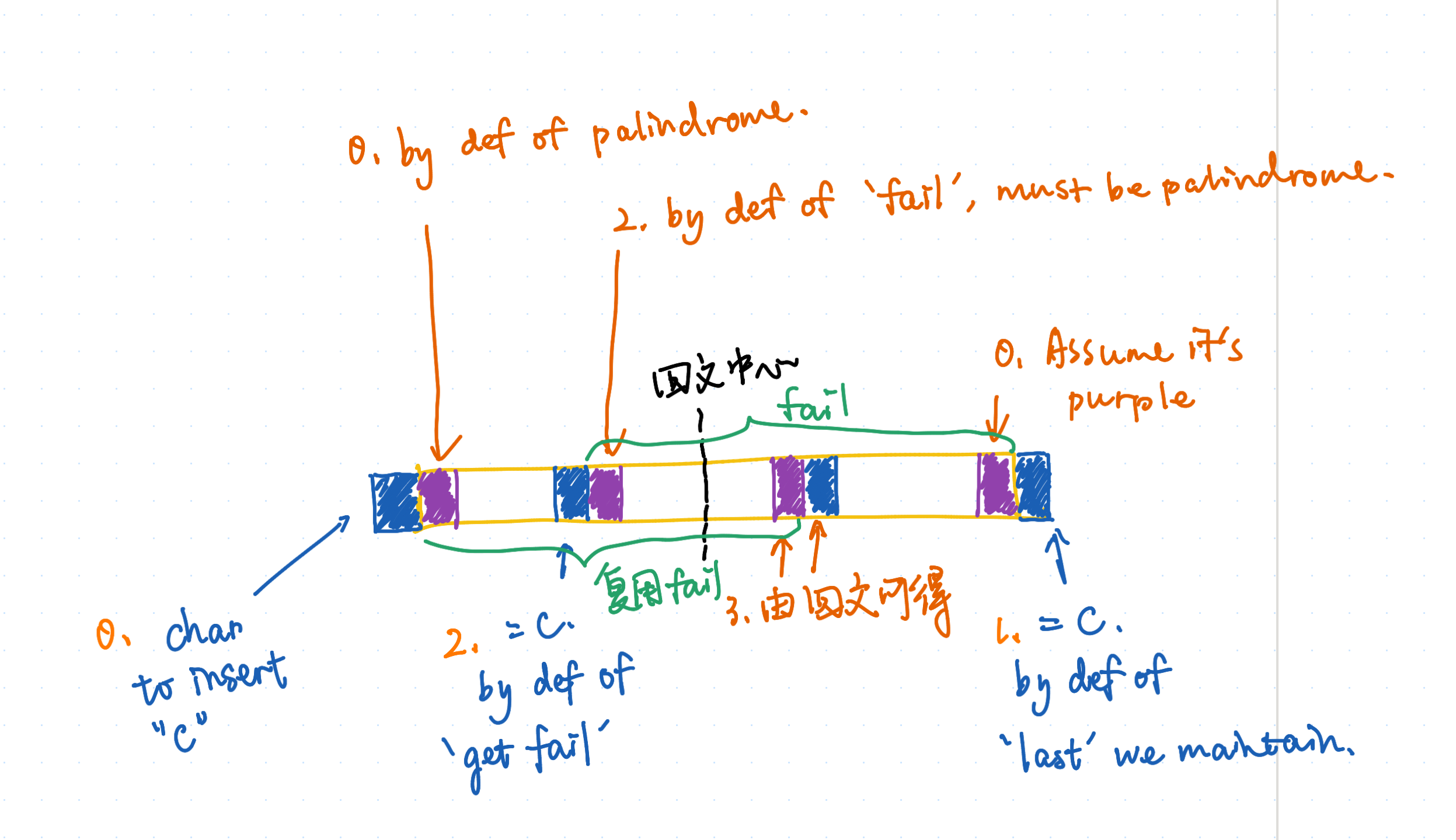
我们考虑对 last_front 跳 fail 指针，得到的是什么。根据跳 fail 指针的定义，我们会有

last_front 的跳 fail

考虑 last_front 对应回文串的回文性，于是：

利用回文性和 fail 指针的长度信息

于是我们就可以使用和“在末尾插入字符”同样的思路，维护“在开头插入字符”的操作。

线性时间复杂度证明

证明线性复杂度，我们考虑节点在 fail 树上的深度。