RoPE

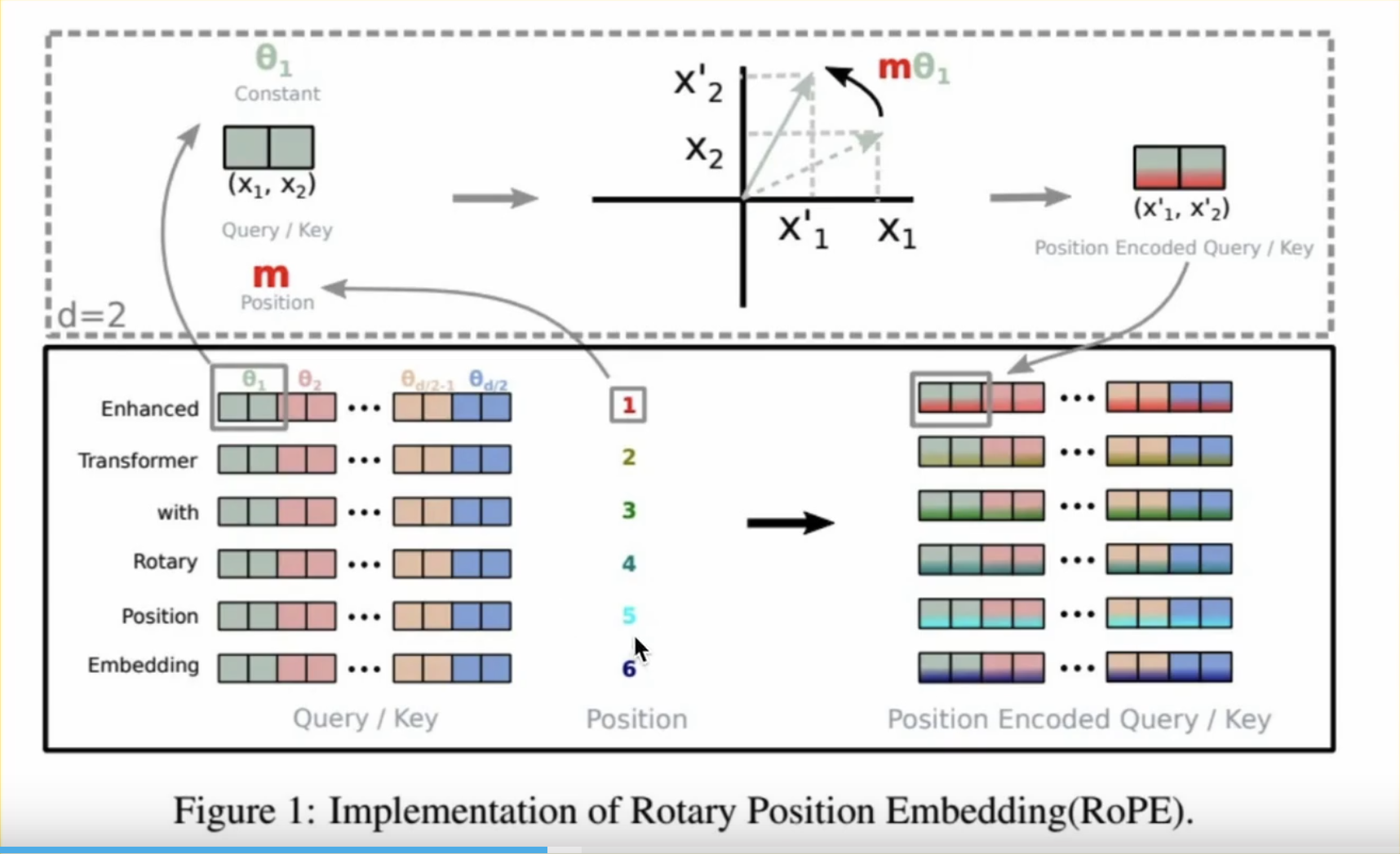
旋转位置编码

旋转位置编码的核心诉求就是需要让 embedding 同时体现出相似度和相对位置这两个信息

我们先考虑如果 $Q,K$ 都只是二维向量，即

那么通常的 Scaled Dot Product Attention 的计算结果应为 $QK^T=ac+bd$，考虑写成复数的话，令 $c_q=a+bi,c_k=c+di$，且 $c_k$ 的共轭为 $c_k^\ast$，则有 $\lang q,k \rang=\Re[c_qc_k^\ast]$，其中 $\Re[c]$ (Latex Code: \real) 表示 $c$ 的实数部分，$\Im[c]$ 表示 $c$ 的虚数部分 (Latex Code: \image)。

我们假设 $\text{RoPE}(x,i)$ 可以表示为复数形式，即 $\text{RoPE}(x,i)=a_x+b_xi=R_x e^{i\theta(x,i)}$，这里第二个等号是复数的指数表示法。

RoPE

虽然论文里是要求对 $x_m^{2i}$ 与 $x_m^{2i+1}$ 加上 $\cos,\sin$ 的 embedding，不过从数学的角度来说，这里的配对实际上不影响最终的结果，“不同的配对方式本质上不影响模型的表达能力，并且可以相互转化”。因此在工程上，考虑到内存连续性，我们通常不用这种相邻配对，而是 $x^{i}$ 与 $x^{i+d/2}$ 进行配对计算。