单变量无约束非线性优化问题

Non-Linear Programming: Problem Formulation

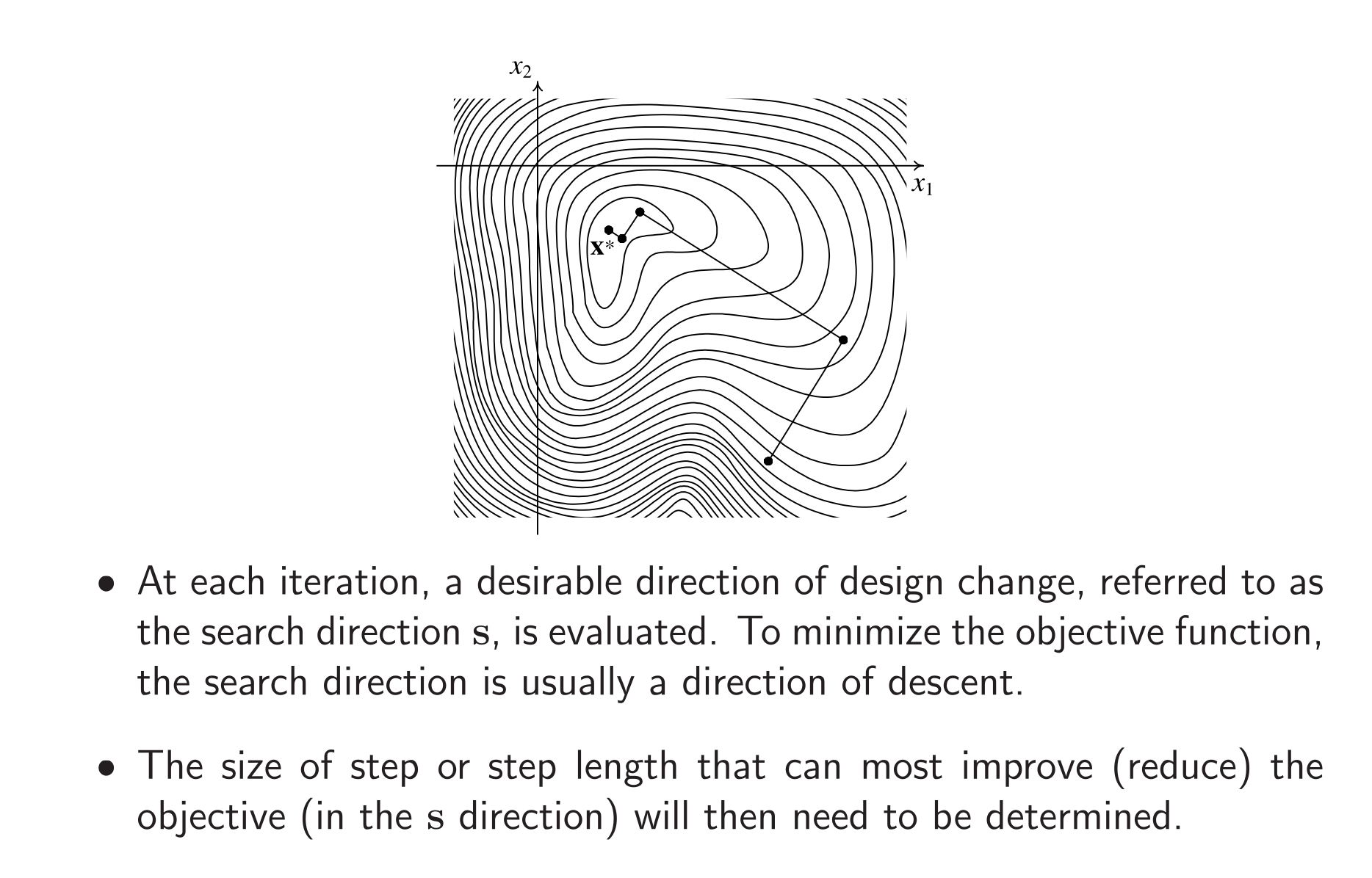
和 Gradient Descent 的过程感觉非常相似……令 $\bold x^{(q)}$ 是当前点， $\bold s^{(q)}$ 是搜索方向， $q$ 是 Iteration 次数，我们就是希望找一个步长 $\alpha$

\begin{aligned} \bold x^{(q+1)}&=\bold x^{(q)} + \Delta \bold x^{(q)}\\ &=\bold x^{(q)}+\alpha \bold s^{(q)}, \alpha\ge 0 \end{aligned}

并且我们把 $g(\alpha)=f(\bold x+\alpha\bold s)$ 看作是关于 $\alpha$ 的函数，我们希望找到的步长 $\alpha^\ast$ 可以最小化这个 $g(\alpha)$

假设 $g(\alpha)$ 的最小值点存在，并且在 $\alpha$ 的定义域内是 唯一 (unimodal) 的

不过，很有可能 $g(\alpha)$ 存在其他极小值点。在数值优化方法里，通常分为两个步骤：

给定单变量函数 $f(x)$ ，我们可以希望 bracket the interval containing the minimum point，一种方式是通过搜索

我们钦定 $\delta\gt 0$ ，然后对 $x=i\delta, i\in\N$ 分别计算 $f(x)$ . 然后，我们可以通过 $f(x)$ 的变化情况判断出 $x^\ast$ 所在的范围。即找到 $s\in N$ 使得

f((s-1)\delta) \ge f(s\delta) \texttt{ and } f(s\delta) \le f((s+1)\delta)

于是我们可以判断出 $x^\ast$ 的范围：

(s-1)\delta \le x^\ast \le (s+1)\delta

和 Equal Interval Search 类似，我们固定下 $\delta$ 后，我们让后续的 interval 长度以 $a$ 的比例增长，即

\begin{aligned} x^{(s+1)}&=x^{(s)}+a^s\delta, s\in\N\\ &=\delta\cdot \sum_{i=0}^s a^i \end{aligned}

最小值所在区间的确定和 Equal Interval Search 也是一样的，即找到 $s$ 使得

f(x^{(s-1)})\ge f(x^{(s)})\texttt{ and }f(x^{(s)})\le f(x^{(s+1)})\\ \implies x^{(s-1)}\le x^\ast \le x^{(s+1)}

那么这个 $a$ 怎么取呢？一种是黄金分割搜索，即 $a=\frac{1+\sqrt{5}}{2}$ .

这一块的任务是在单谷函数里找最小值（和算法竞赛里的三分很像）

我们不断在 $[x_l, x_r]$ 的区间里选取两个点

x_1=\varphi\cdot x_l + (1-\varphi)\cdot x_r\\ x_2=(1-\varphi)\cdot x_l + \varphi\cdot x_r

其中 $\varphi=\frac{\sqrt{5}-1}{2}$ .

所以我们接着比较 $f(x_l), f(x_1), f(x_2), f(x_r)$ ，并且不断收紧 $[x_l, x_r]$ . 每次收紧，可以舍弃 $\varphi$ 的部分，时间复杂度 $O(\log V)$ .

我们之所以使用 $\varphi$ 作为分割比例，是因为下一次的迭代可以复用计算出来的函数值。例如，第一次迭代中 $[x_l, x_r]$ 收窄为了 $[x_l, x_2]$ ，在第二次迭代里，第一次迭代中的 $x_1$ 就是下一次迭代里的 $x_2'$ .

我们考虑三分搜索的终止条件，我们可以设立一个 error tolerance $\epsilon_{lr}$ ，只要上下界的绝对误差或者相对误差小于 $\epsilon_{lr}$ 即可停止

\frac{x_r-x_l}{x_r^{(0)}-x_l^{(0)}}\le \epsilon_{lr}\texttt{ or } x_r-x_l\le \epsilon_{lr}

此时我们令最小值点为其中点

x^\ast=\frac{x_l+x_r}{2}

Polynomial Approximation 的核心思想是用一个多项式去拟合原函数 $f(x)$ ，当拟合程度比较高的时候，我们可以认为我们选择的这个多项式的最小值点比较 approximate $f(x)$ 的最小值点了。

Quadric Approximation

我们先来考察多项式为二次的时候。对于二次多项式 $g(x)=a_0+a_1x+a_2x^2$ ，我们需要三个点来计算其系数，我们取 $x_l, x_{\text{mid}}, x_r$ . 其中 $x_{\text{mid}}=\frac{x_l+x_r}{2}$

于是我们可以计算出多项式的最低点

x^\ast=-\frac{a_1}{2a_2}, a_2\gt 0

所以我们可以计算出四个点的取值 $x_l, x^\ast, x_{\text{mid}}, x_r$ ，然后和 Golden Section Method 类似，我们可以不断收紧区间 $[x_l, x_r]$

当连续两次的 $x^\ast$ 足够接近的时候，我们就可以停止了，即

|x^{\ast(r+1)}-x^{\ast(r)}|\le \epsilon_x

其中 $\epsilon_x$ 是事先约定好的误差， $r\in\N$ 是迭代次数。