Pareto Optimality

在多目标优化问题里，我们虽然很难确定什么是最优解，但我们可以判定什么解不是最优解. 这个想法衍生出 Pareto Optimality 做法.

Pareto Optimality

以双变量双目标优化问题为例

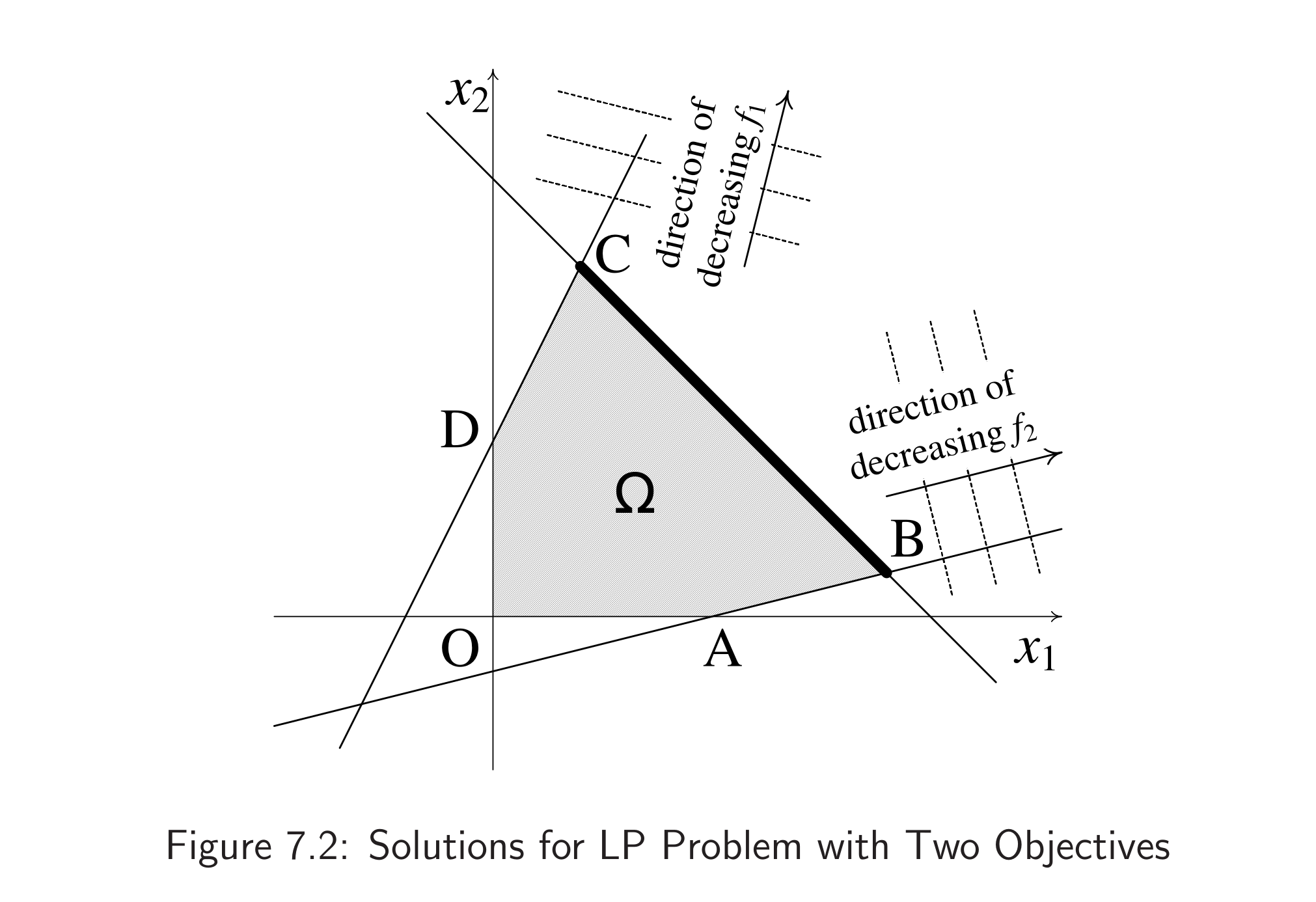
如果我们只关心 $f_1$ ，那么 $C$ 就是 Optimal Point；反之，如果只关心 $f_2$ 那么 $B$ 才是那么 optimal point.

而现在，我们并不确定更关心 $f_1，f_2$ 中的哪一个，所以其实 $BC$ 线段上的每一个点都有可能成为 optimal point. 所以，我们把 $BC$ 上的每一条点都记为 Pareto (Optimal) Points.

如果我们把坐标系换成 $f_1 f_2$ 坐标系

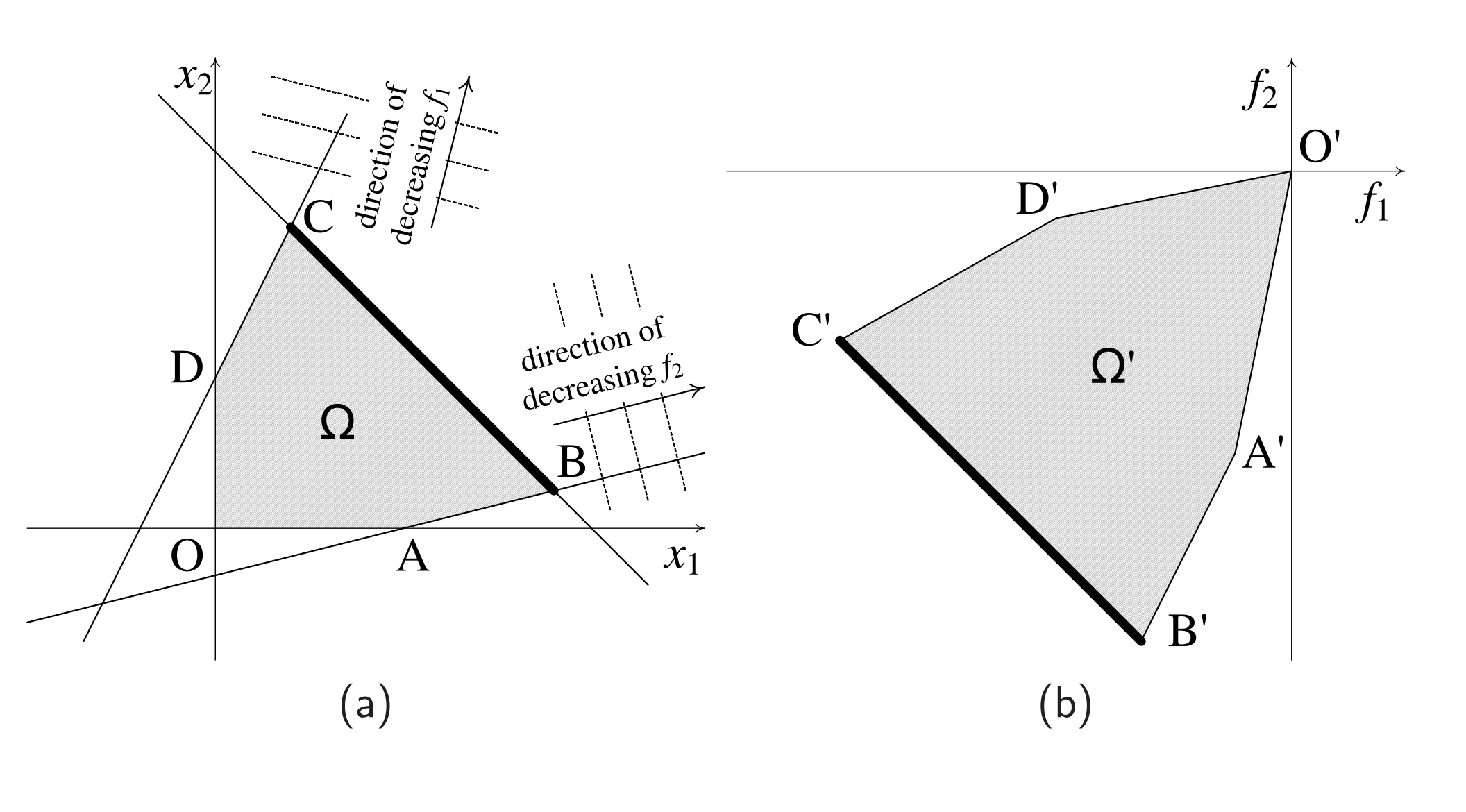
$图中的 $B'C'$ 就是 Pareto Points，因为找不到其他点可以同时降低 $f_1,f_2$. 我们把这样的 $B'C'$ 称为 **Pareto frontier**$

图中的

B'C'

就是 Pareto Points，因为找不到其他点可以同时降低

f_1,f_2

. 我们把这样的

B'C'

称为 Pareto frontier

我们把上面的例子拓展到 $m$ 维（即 $m$ 个目标函数），则

Pareto Optimality

一个解 $\bold{x}^\ast \in\Omega$ 是 Pareto optimal 的，当且仅当不存在其他解 $\bold{x}\in\Omega$ 满足

f_j(\bold{x})\le f_j(\bold{x}^\ast), \text{ for all }j\in[1,m]

f_i(\bold{x})\lt f_i(\bold{x}^\ast), \text{ for at least one }i\in[1,m]

简言之，就是不存在另外一个点，它即能保持所有其他 $f_j$ 不增大，又能把一个 $f_i$ 减小.

Generation and Visualization

那么我们怎么找这些 Pareto points 呢？一个解决办法是，多次使用 $\varepsilon$ -Constraint 法（多次调整 $\varepsilon_j$ ）或者 weighted sum 法（多次调整权重）.

the entire Pareto frontier can theoretically be generated if the set of limits/weights can be continuously varied and the problem repeatedly solved.

但如果目标函数是 non-convex 的，那么很有可能传统方法就无法找出 pareto frontiers 了. 因为这些传统方法本质上还是只优化一个目标函数，而 pareto frontier 需要考虑多个目标函数.

所以这个时候一些遗传算法 (evolutionary techniques) 就有用武之地了. 当我们维护多个解，这意味这我们可以在一次迭代里同时优化多个目标函数.

值得注意的是，如果某些新点加入，使得原来的 pareto points 被 dominated 了，那么这些点应该被移除；而且相应的，原来的、被 dominated pareto points 所 dominate 的点可能需要重新加入集合. 基于这一观察，我们可以提出 pareto ranking scheme.

我们把最外围的 pareto points 打上 rank $1$ ，然后移除他们，在剩下的点里再找出 pareto points，打上 rank $2$ ……直到所有点都被打上了 rank.

另一个算法是，每个点的 rank $=1+\#\{\text{points dominating it}\}$

这个 rank（或者再套个函数）适合作为遗传算法里的 fitness. 如果最终的解集数量足够，并且在 objective space 里分布良好，那么我们可以从这些点里识别出 pareto frontier. 如果问题是离散的，那么 objective space 里的接近程度可能并不对应 variable space 中的接近程度.