人类穷极一切都在努力让计算机拥有人类一般的视觉能力. 然而早期的计算机只能深陷“平面”的囹圄之中：在计算机里，图像都是以矩阵、张量保存，最多编码色彩信息，而无法编码立体信息（如某个物体离我多远？）.

为了克服这些问题，让计算机拥有人类一般的视觉能力，那么我们让计算机也像人类那样拥有两只“眼睛”不就好了？人类为计算机配上两个摄像机，结合数学知识，用两个摄像机模拟人类的双目视觉，让计算机也可以拥有人类一般的“深度感知”能力 (depth perception).

Stereo Vision

我们人类的双眼本质和计算机的两个摄像头没有任何区别，都是将立体的现实投影成二维的平面. 我们是怎么“感觉”到物体离我们的远近呢？

坐在运动的车内向车外看去，一般都能看到远处的物体好像运动得越慢，近处的物体好像运动得更快. 这个现象就是启发：假设车运动一秒，在我的视角下，视野内的物体会运动不同的距离，运动距离越大的物体离我越近，运动距离越小的物体离我越远.

对于静止的人眼，两眼之间的距离就是天然的“车运动一秒的距离”，所以左眼与右眼同时向前看一个物体，由于左眼与右眼不在同一个位置上（双眼之间有距离），其在左眼成像里的位置和其在右眼所成像的位置是不一样的（即前文物体运动距离的比喻）. 于是，我们的大脑会自动对这两张图像进行“拟合”，把物体的位置重合.

对于计算机视觉，我们就需要将大脑的拟合过程用数学公式描述下来. 在计算机视觉里，深度 (depth) 指的就是物体到两个摄像头中心的距离，视差 (disparity, parallax) 前者指的是同一个物体在两张图像里位置的差值（后者则通常指一个现象）.

如何从视差推理深度？三角视差法

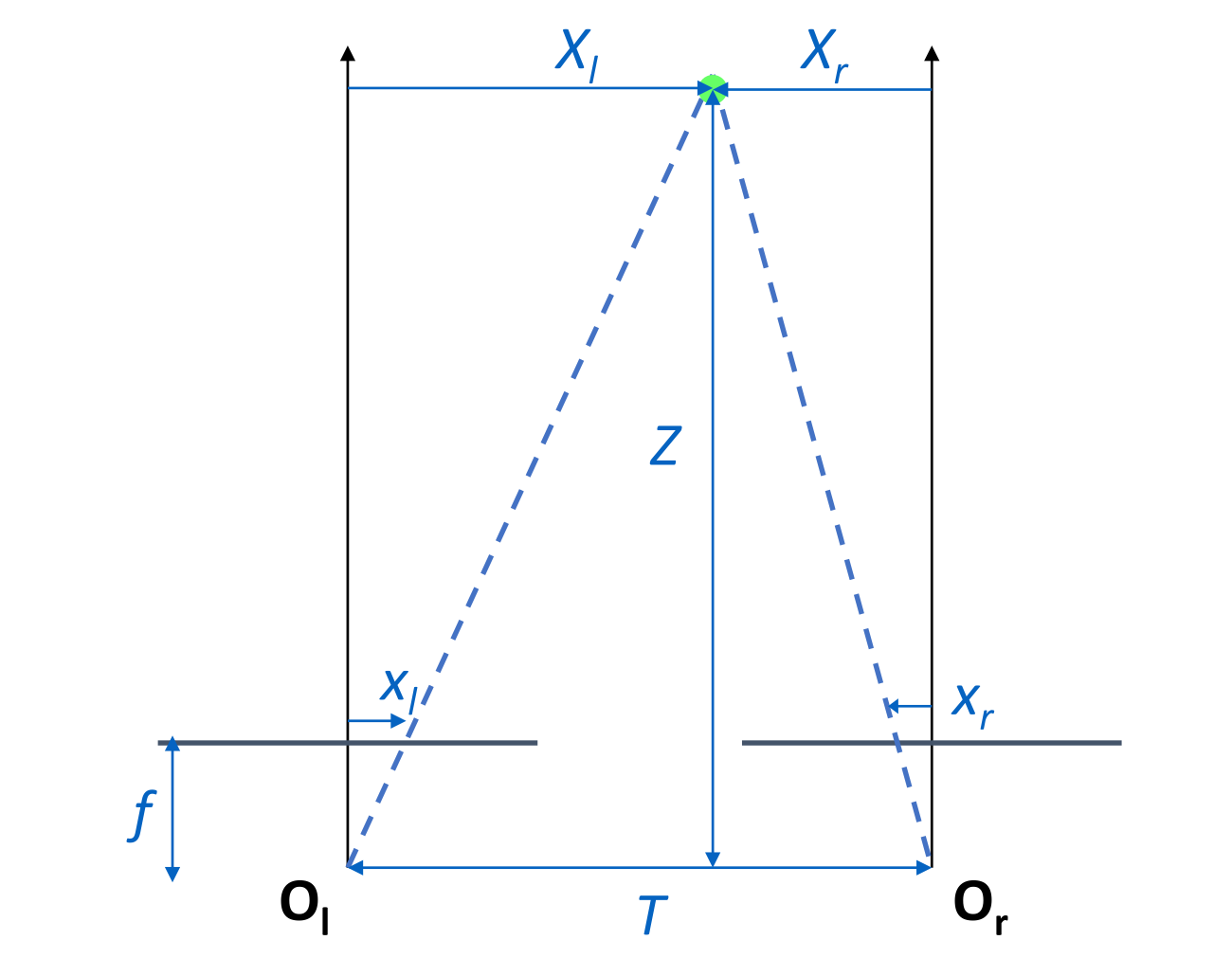
我们考虑相机之间距离为 TT. 且为针孔相机，焦距为 ff，物体距离相机的深度为 ZZ. 以下的向量中 Xl,xl>0X_l,x_l\gt 0 表示在轴的右侧，Xr,xr>0X_r,x_r\gt 0 表示在轴的左侧

从图中可知，视差（物体位置变化量）为 d=xl−xrd=x_l-x_r，根据相似，有

XlZ=xlfXrZ=xrf \frac{X_l}{Z}=\frac{x_l}{f}\\ \frac{X_r}{Z}=\frac{x_r}{f}

且 Xl−Xr=TX_l-X_r=T. 所以

Zd=fT Zd=fT

Point Matching

Point Matching 无论是 Appearance-Based 还是 Feature-Based，其核心思想都是：左右眼的图像应该相差不多，故对于左眼图像上的一个部分 PlP_l，在右眼图像中，我们应该可以找到一个部分 Pr^\hat{P_r} 它和 PlP_l 应该是相似的.

视差图

视差图指的是对于左眼图的某个像素与右眼图里匹配的像素之间位置的差距. 即对于左眼图 Pl=(x,y)P_l=(x,y)，若其在右眼图的匹配为 Pr^=(x′,y′)\hat{P_r}=(x',y')，则视差图中 D(x,y)=∥Pl−Pr^∥2D(x,y)=\|P_l-\hat{P_r}\|_2

Appearance-Based Method

这个方法适用于左右眼图像形变较少的，比如说左右眼的图像的差距只有简单平移.

基于“双眼图像之间只有简单平移”的 heuristics，我们可以用一个简单的方法计算视差.

  1. 对于左眼图的某个像素，提取周围 h×wh\times w 的 window.

  2. 由于只有简单的平移，我们假设最大的位移距离为 dmax⁡d_{\max}. 则我们在右眼图 x′∈[x−dmax⁡,x+dmax⁡],y′∈[y−dmax⁡,y+dmax⁡]x'\in[x-d_{\max},x+d_{\max}], y'\in [y-d_{\max},y+d_{\max}] 共计 (2dmax⁡+1)2(2d_{\max}+1)^2 个像素的这个区域里，对于 (x′,y′)(x',y') 也先提取出周围 h×wh\times w 的 window，然后计算 Sum of Square Difference.

    ∑u=−⌊h2⌋⌊h2⌋∑v=⌊w2⌋⌊w2⌋[L(x+u,y+v)−R(x′+u,y′+v)]2 \sum_{u=-\lfloor\frac{h}{2}\rfloor}^{\lfloor\frac{h}{2}\rfloor}\sum_{v=\lfloor\frac{w}{2}\rfloor}^{\lfloor\frac{w}{2}\rfloor} \Big[ L(x+u,y+v)-R(x'+u,y'+v) \Big]^2

  3. 在右眼图区域内的所有像素里，我们令最小的 SSD\text{SSD} 对应的那个像素 (x0′,y0′)(x'_0,y'_0) 和 (x,y)(x,y) 匹配. 即

    arg min⁡x′,y′∑u=−⌊h2⌋⌊h2⌋∑v=⌊w2⌋⌊w2⌋[L(x+u,y+v)−R(x′+u,y′+v)]2 \argmin_{x',y'} \sum_{u=-\lfloor\frac{h}{2}\rfloor}^{\lfloor\frac{h}{2}\rfloor}\sum_{v=\lfloor\frac{w}{2}\rfloor}^{\lfloor\frac{w}{2}\rfloor} \Big[ L(x+u,y+v)-R(x'+u,y'+v) \Big]^2

这个算法被称为 Sum of Square Difference (SSD) 算法. 这一过程的朴素实现需要使用 33 个 for 循环，我们可以用矩阵更加快速地进行实现（同时 MATLAB, Python 等的数学库对于矩阵运算都有加速支持，效率上也有提升）

矩阵加速 SSD 算法

上面算法的思路简述一下是“枚举像素找 dd”. 如果可以确保只有水平移动，我们可以变换思路：枚举 dd 找哪些像素的视差等于 dd.

所以我们枚举视差 dd，然后将右眼图向左或向右（取决于 dd 的正负）平移，这样 L(x,y)L(x,y) 周围 h×wh\times w 的 window 和 R(x+d,y)R(x+d, y) 的 window 就对齐了. 同时 sum of square difference 可以化简为

∑windowL(x,y)2+∑windowR(x+d,y)2−2∑windowL(x,y)R(x+d,y) \sum_{\text{window}} L(x,y)^2 + \sum_{\text{window}} R(x+d,y)^2-2\sum_{\text{window}} L(x,y)R(x+d,y)

前两项相当于是将 M(x,y)←M(x,y)2M(x,y)\gets M(x,y)^2 后对长宽为 h×wh\times w 的 全 11 矩阵进行卷积，后面一项则是先将 L,RL,R 两个矩阵逐元素相乘后再对全 11 矩阵进行卷积.

这样我们就对所有像素计算了在视差为 dd 的情况下，像素的 SSD 值. 我们开一个大小为 H×W×dmax⁡H\times W\times d_{\max} 的矩阵，保存下 dd 时的 SSD 值. 最后再对每一个像素在 dd 轴取 arg min⁡\argmin，即可算出每一个像素的视差了.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
function [disparity] = matrix_ssd(L, R, h, w)
    [H, W] = size(L);
    window = ones(h, w);

    maxd = 15;

    costmap = inf(H, W, maxd * 2 + 1);
    sqrL = conv2(L .^ 2, window, 'same');

    function [mx] = rshift(mat, d)
        mx = inf(size(mat));

        if d >= 0
            mx(:, d + 1:end) = mat(:, 1:end - d);
        else
            mx(:, 1:end + d) = mat(:, 1 - d:end);
        end

    end

    for d = -maxd:maxd
        Rp = rshift(R, d);
        sqrR = conv2(Rp .^ 2, window, 'same');
        cross = conv2(L .* Rp, window, 'same');

        ssd = sqrL + sqrR - 2 * cross;
        costmap(:, :, d + maxd + 1) = ssd;
    end

    [~, bestd] = min(costmap, [], 3);
    disparity = bestd - maxd - 1;
end

Feature-Based Method

适用于形变较大的情况. 例如两个摄像头之间还有旋转.

Feature-Based 方法相比于 Appearance-Based 方法的区别在于几点

  1. Appearance-Based 使用的是左眼图像的方形区域作为 pattern 和右眼图像进行匹配；而 Feature-Based 方法则先使用 Scale Invariant Feature Transform (SIFT) 找出图像里的 feature point，然后再将其配对.
  2. 假设 PlP_l 配对上了 PrP_r，那么我们依然可以利用 Triangulation 计算出物体的坐标.

3D Reconstruction

相机的本质上是一个矩阵线性投影，将一个 3D 向量投影到 2D 平面上

CL=CamL:[kxlkylk]=[a1a2a3a4a5a6a7a8a9a10a111][XYZ1]CR=CamR:[mxrmyrm]=[b1b2b3b4b5b6b7b8b9b10b111][XYZ1] C_L=\text{Cam}_L: \begin{bmatrix}kx_l \\ ky_l \\ k\end{bmatrix}=\begin{bmatrix}a_1&a_2&a_3&a_4\\ a_5&a_6&a_7&a_8\\ a_9&a_{10}&a_{11}&1 \end{bmatrix}\begin{bmatrix} X\\ Y\\ Z\\1 \end{bmatrix} \\ C_R=\text{Cam}_R: \begin{bmatrix}mx_r \\ my_r \\ m\end{bmatrix}=\begin{bmatrix}b_1&b_2&b_3&b_4\\ b_5&b_6&b_7&b_8\\ b_9&b_{10}&b_{11}&1 \end{bmatrix}\begin{bmatrix} X\\ Y\\ Z\\1 \end{bmatrix}

这个 3×43\times 4 的矩阵是相机的参数矩阵，如果我们可以知道这两个相机的参数矩阵，那么未知量就只有 X,Y,ZX,Y,Z，而 xl,yl,xr,yrx_l,y_l,x_r,y_r 也是已知的，我们就可以解出 X,Y,ZX,Y,Z 了.

参数矩阵？

实际上，这个参数矩阵包含了四个坐标系之间的转化：世界坐标系 →\to（刚体变换） 相机坐标系 →\to（透视投影） 图像坐标系 →\to（二次转换） 像素坐标系. 从矩阵的角度说，包含了内参矩阵、外参矩阵、畸变参数.

我们怎么解出这个参数矩阵呢？上面的过程反过来，如果我们可以人为确定好 X,Y,ZX,Y,Z 的坐标，然后测量 xr,yr,xl,ylx_r,y_r,x_l,y_l 那么我们也可以反解出 CL,CRC_L,C_R.

这个过程称为相机标定 (Camera Calibration)：

  1. 我们固定好两个相机的位置
  2. 然后我们用标定板对相机进行标定. 因为使用了标定板，所以三维坐标可以认为是已知的. 进而反解出参数矩阵.

然后就可以利用视差进行 3D 重建了.

通过列方程，我们最后可以得到这样的方程

[a9xl−a1a10xl−a2a11xl−a3a9yl−a5a10yl−a6a11yl−a7b9xr−b1b10xr−b2b11xr−b3b9yr−b5b10yr−b6b11yr−b7][XYZ]= [a4−xla8−ylb4−xrb8−yr] \begin{bmatrix} a_9 x_l - a_1 & a_{10} x_l - a_2 & a_{11} x_l - a_3 \\ a_9 y_l - a_5 & a_{10} y_l - a_6 & a_{11} y_l - a_7 \\ b_9 x_r - b_1 & b_{10} x_r - b_2 & b_{11} x_r - b_3 \\ b_9 y_r - b_5 & b_{10} y_r - b_6 & b_{11} y_r - b_7 \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \end{bmatrix} =\ \begin{bmatrix} a_4 - x_l \\ a_8 - y_l \\ b_4 - x_r \\ b_8 - y_r \end{bmatrix}

记左侧 4×34\times 3 的矩阵为 WW，右侧的四维向量为 qq. 我们可以用 pseudo-inverse 解出 X,Y,ZX,Y,Z 的值：

[XYZ]=W+q=(W⊤W)−1W⊤q \begin{bmatrix} X \\ Y \\ Z \end{bmatrix} = W^+ \mathbf{q} = (W^\top W)^{-1} W^\top \mathbf{q}

Deep Stereo Vision

这一部分介绍一点时间稍微早一点的工作，用深度学习解决立体视觉的问题.

License

本文采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议，转载请注明出处。