Quadric Surfaces

Quadric Surfaces 是由三元二次方程确定的曲面：

ax2+by2+cz2+dxy+exz+fyz+gx+hy+lz+m=0ax^2+by^2+cz^2+dxy+exz+fyz+gx+hy+lz+m=0

Quadric Surfaces 包含很多特殊情况，例如椭圆体（包括球体）、椭圆抛物面、双曲抛物面、单叶双曲面、双叶双曲面、圆锥、椭圆柱面（包括圆柱体）、双曲柱面、抛物柱面。我们先研究其中的几个。

Sphere 球体

  • 隐函数形式：x2+y2+z2−r2=0x^2+y^2+z^2-r^2=0
  • 参数方程：
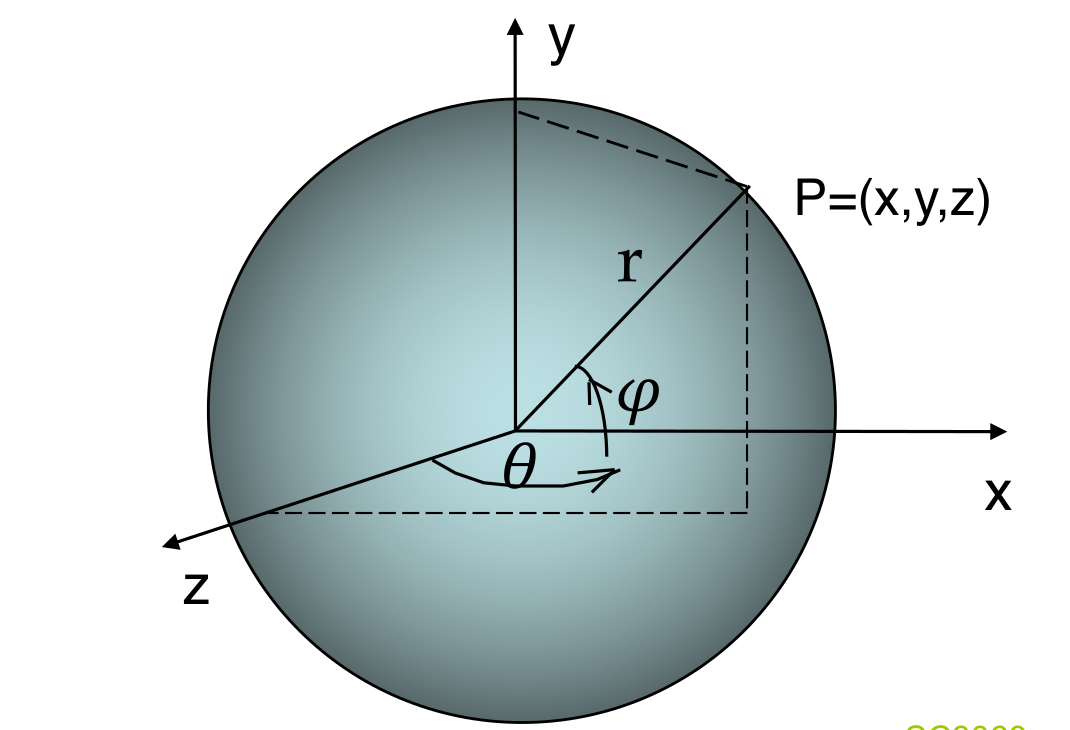
x=rcos⁡ϕsin⁡θy=rsin⁡ϕz=rcos⁡ϕcos⁡θϕ∈[−π2,π2],θ∈[−π,π] x=r\cos\phi\sin\theta\\ y=r\sin\phi\\ z=r\cos\phi\cos\theta\\ \phi\in[-\frac{\pi}{2},\frac{\pi}{2}], \theta\in[-\pi, \pi]

只需要看准 θ,ϕ\theta, \phi 分别对应的是什么角即可

Epllisoid 椭圆体

  • 隐函数形式：(xa)2+(yb)2+(zc)2−1=0(\frac{x}{a})^2+(\frac{y}{b})^2+(\frac{z}{c})^2-1=0
  • 参数方程形式（相比于球体，就是把 rr 换成三个轴上的轴长 a∗,b∗,c∗a^\ast,b^\ast,c^\ast）
x=a∗cos⁡ϕsin⁡θy=b∗sin⁡ϕz=c∗cos⁡ϕcos⁡θϕ∈[−π2,π2],θ∈[−π,π] x=a^\ast \cos\phi\sin\theta\\ y=b^\ast \sin\phi\\ z=c^\ast \cos\phi\cos\theta\\ \phi\in[-\frac{\pi}{2},\frac{\pi}{2}], \theta\in[-\pi, \pi]
图形学基础/曲面
License

本文采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议，转载请注明出处。