经典 Transformer 架构

Transformer Architecture

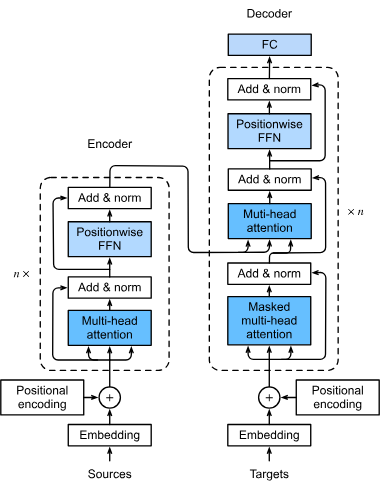
经典的 Transformer 架构

从整体的架构来看，Transformer 由 Encoder 和 Decoder 两个部分组成.

Encoder

对于输入数据 $\bold{x}$ ，Embedding 完后，我们先做一次 Positional Encoding $\bold{x}'\gets \bold{x}+\bold{P}(\bold{x})$ .

紧接着，张量 $\bold{x}'$ 会经过多个 stacked layers，每一个 layer 包含两个 sublayers:

首先经过 Multi-Head Self Attention 以及 Residual Connection & Layer Norm
其次经过 Fully Connected Network (FCN) 以及 Residual Connection & Layer Norm

我们设计了 Add and Layer Normalization，所以，我们的 FCN 和 Attention 输出的词向量维度应该和输入词向量维度一致，即 $\bold{x}\in\R^d$ 并且 $\bold{x}+\text{sublayer}(\bold{x})\in\R^d$

于是，Transformer 的 Encoder 为句子里的每一个位置输出一个 $d$ 维词向量表示.

Decoder

Transformer Decoder 部分也是 stack of layers. 同样，在 embedding 完后，我们先做一次 Positional Encoding. 然后依次经过

Masked Multi-Head Self Attention, Residual Connection & Layer Norm

这里为什么是 Masked 呢？这与 Transformer 生成答案的过程有关.

我们知道，Transformer 在生成 token 的时候是 autoregressive 的，即生成第 $i$ 个 token 的时候，它不知道 $i+1\to\infin$ 个 token 是长什么样的，只知道 $1\to i-1$ 个 token. 所以我们需要 mask 把 $i+1\to \infin$ 号 token 的 score 设置为 $0$ .
Encoder-Decoder Multi-Head Attention, Residual Connection & Layer Norm

这里的特殊之处在于，Query 是上一层 Masked Multi-Head Self Attention 的输出，KV 则是来自 Encoder 的输出.

其意义（感性地理解）差不多是，我们已经知道了目标语言的句子的关联，现在是时候把目标语言的单词和源语言的单词一一对应起来了.
Pointwise FFN, Residual Connection & Layer Norm

Implementation

Pointwise Feed-Forward Networks

Pointwise FFN 将所有句子的单词的词向量表示进行 transformation. 其实就是线性层 + ReLU + 线性层

实现起来也不算很难.

import torch
import torch.nn as nn
from typing_extensions import Optional


class PositionWiseFFN(nn.Module):
    def __init__(self, ffn_hidden_dims: int, ffn_output_dims: int):
        super().__init__()

        self.dense1 = nn.LazyLinear(ffn_hidden_dims)
        self.relu = nn.ReLU()
        self.dense2 = nn.LazyLinear(ffn_output_dims)

    def forward(self, X: torch.Tensor) -> torch.Tensor:
        return self.dense2(self.relu(self.dense1(X)))

Add & Norm

下面的 $\tt{X}$ 表示 sublayer 的输出， $\tt Y$ 表示 residual connection 的输入.

class AddNorm(nn.Module):
    def __init__(self, dim, dropout):
        super().__init__()

        self.dropout = nn.Dropout(dropout)
        self.ln = nn.LayerNorm(dim) # 这里的 dim 一般和最初词向量的维度相同

    def forward(self, X, Y):
        return self.ln(self.dropout(Y) + X)

Encoder Part

Encoder Block

我们先编写单个 Encoder Block，其包含两个 sublayers

class EncoderBlock(nn.Module):
    def __init__(
        self,
        num_hidden: int,
        ffn_dim: int,
        num_heads: int,
        dropout: float = 0.5,
    ):
        super().__init__()

        #
        self.attention = MultiHeadAttention(num_hidden, num_heads, dropout)
        self.addnorm1 = AddNorm(num_hidden, dropout)

        self.ffn = PositionWiseFFN(ffn_dim, num_hidden)
        self.addnorm2 = AddNorm(num_hidden, dropout)

    def forward(
        self,
        X: torch.Tensor,
        valid_lens: Optional[torch.Tensor] = None,
    ) -> torch.Tensor:
        Y = self.addnorm1(X, self.attention(X, X, X, valid_lens))
        return self.addnorm2(Y, self.ffn(Y))

Encoder Module

然后就可以来实现 Encoder 了.

class Encoder(nn.Module):
    def __init__(
        self,
        vocab_size: int,
        num_hidden: int,
        ffn_dim: int,
        num_heads: int,
        num_blocks: int,
        dropout: float,
        use_bias: bool = False,
    ):
        super().__init__()

        self.num_hidden = num_hidden
        self.embedding = nn.Embedding(vocab_size, num_hidden)
        self.pos_emb = PositionalEncoding(num_hidden, dropout)
        self.blocks = nn.Sequential()
        for i in range(num_blocks):
            self.blocks.add_module(
                f"block_{i}",
                EncoderBlock(num_hidden, ffn_dim, num_heads, dropout),
            )

    def forward(
        self,
        X: torch.Tensor,
        valid_lens: Optional[torch.Tensor] = None,
    ) -> torch.Tensor:

        X = self.embedding(X)
        X = self.pos_emb(X * math.sqrt(self.num_hidden))

        self.attn_weights = []
        for i, block in enumerate(self.blocks):
            X = block(X, valid_lens)
            self.attn_weights.append(block.attention.attention.attn_weights)

        return X

为什么 Embedding 后要乘以

\sqrt{d}

这是因为 nn.Embedding 的权重都是随机初始化的，如果使用 Xavier 初始化，则参数服从 $W_{ij}\sim \mathcal{N}(0, \frac{1}{d})$ . 这样导致 embedding vector 的元素通常较小.

而在 Positional Encoding 里面， $\cos, \sin$ 等三角函数的值在 $[-1,1]$ 之间，如果 nn.Embedding 的值过小，那么相加后，结果将由 Positional Encoding 主导. 几乎相当于是原句子全部被舍弃，只有位置信息在参与后续的意义关联（

所以，我们需要人为地提升 embedding 的值的 scaling，故我们 $\times \sqrt{d}$ ，这样， $\text{Var}=1$ ，量级就和 Positional Embedding 差不太多了.

Decoder Part

Decoder Block

class DecoderBlock(nn.Module):
    def __init__(
        self,
        num_hiddens: int,
        ffn_dim: int,
        num_heads: int,
        dropout: float,
        i: int,
    ):
        super().__init__()

        self.i = i  # block index

        # masked multi-head self-attention
        self.attn1 = MultiHeadAttention(num_hiddens, num_heads, dropout)
        self.addnorm1 = AddNorm(num_hiddens, dropout)

        # multi-head cross-attention
        self.attn2 = MultiHeadAttention(num_hiddens, num_heads, dropout)
        self.addnorm2 = AddNorm(num_hiddens, dropout)

        # position-wise feed-forward network
        self.ffn = PositionWiseFFN(ffn_dim, num_hiddens)
        self.addnorm3 = AddNorm(num_hiddens, dropout)

    def forward(
        self,
        X: torch.Tensor,
        state: tuple[torch.Tensor, torch.Tensor, Dict],
    ) -> tuple[torch.Tensor, tuple]:
        """State 就是从 Encoder 传过来的 context & valid_lens."""
        enc_output, enc_valid_lens = state[0], state[1]

        # kv cache
        if state[2][self.i] is None:
            key_values = X
        else:
            key_values = torch.cat((state[2][self.i], X), dim=1)
        state[2][self.i] = key_values

        if self.training:
            batch, num_steps, dim = X.shape
            decoder_visible_mask = torch.arange(
                1,
                num_steps + 1,
                device=X.device,
            ).repeat(batch, 1)
        else:
            decoder_visible_mask = None

        # masked multi-head self-attention
        X2 = self.attn1(X, key_values, key_values, decoder_visible_mask)
        Y = self.addnorm1(X, X2)

        # multi-head cross-attention
        Y2 = self.attn2(Y, enc_output, enc_output, enc_valid_lens)
        Z = self.addnorm2(Y, Y2)

        return self.addnorm3(Z, self.ffn(Z)), state

这一段代码的 __init__() 还是比较易懂的，基本上就是和之前的结构图对应上了.

然而在 forward() 里面有点细节。首先 $\tt state$ 保存了三个信息：

$\texttt {state}_0$ 保存 encoder block 的输出；
$\texttt{state}_1$ 保存的是源序列的有效长度；
$\texttt{state}_2$ 保存的是 caches per layer（每层保存“到目前为止已解码 token”的键值缓存）

首先读这一段代码：训练时，一次性输入一整串目标序列，所以 state 直接保存完整序列；而在推理的时候，每一步都会新增一个 token，于是用 torch.cat 拼接起来

if state[2][self.i] is None:
    key_values = X
else:
    key_values = torch.cat((state[2][self.i], X), dim=1)
state[2][self.i] = key_values

接下来看这段代码：如果是训练，那么我们需要构造严格的 masking 让 $t$ 位置上的 token 看不到 $t+1\to \infin$ 位置上的 token；但如果是推理，由于本身就是 autoregressive 的，state 只会保存以前的 token，于是就不需要特殊设置 masking 了。

if self.training:
    batch, num_steps, dim = X.shape
    decoder_visible_mask = torch.arange(
        1,
        num_steps + 1,
        device=X.device,
    ).repeat(batch, 1)
else:
    decoder_visible_mask = None