![]()
圆的数据结构定义
1
2
3
4
| struct circle {
point c;
real r;
};
|
注意事项
- 尽量避免直接用
(long) double 进行操作,考虑到浮点误差,更建议使用向量操作
圆与直线
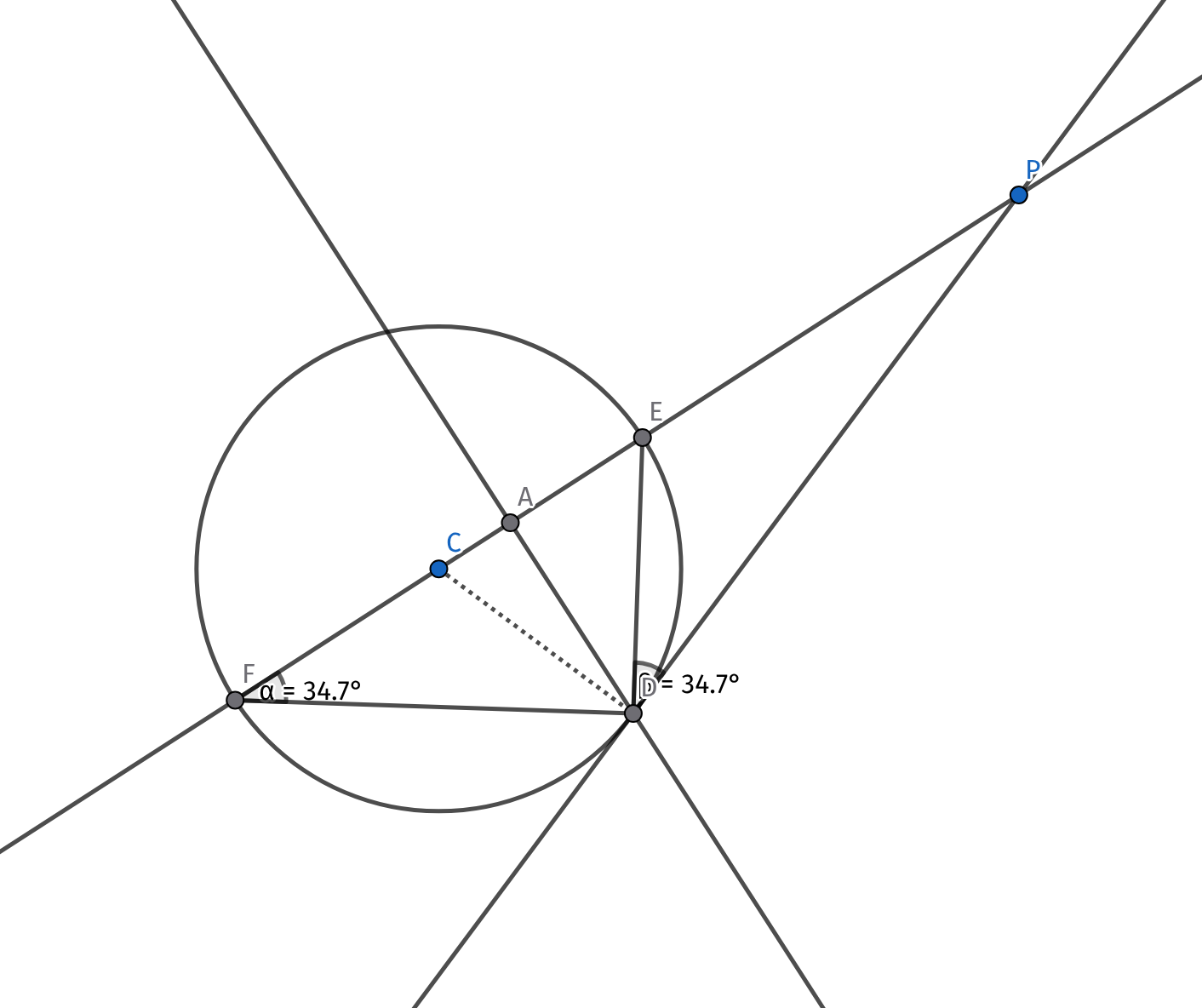
过某点做某圆的切线
过一个点 P 做圆 C 的切线
若点 P 在圆上,则切线垂直于半径 CP,直接令直线 s=P, d=perp(CP).
否则 P 在圆外,否则没有切线。此时有两条切线,且应当关于 CP 对称。考虑用误差更小的向量组合求出 D,然后另一边也能求了。
令 ∣CP∣=d,推理 ΔPCD 的面积,发现 ∣AD∣=drd2−r2,∣AP∣=dd2−r2
所以 D=P+∣AP∣⋅PC±∣AD∣⋅perp(PC)
Reference Code
1
2
3
4
5
6
7
8
9
10
11
12
| std::vector<line> tangent(point x, circle c) {
real d = distance(c.c, x);
std::vector<line> res = {};
if (d == c.r) res.push_back(line{x, perp(c.c - x)});
else if(d > c.r) {
real c1 = (d.sqr() - c.r.sqr()) / d;
real c2 = c.r * (sqrt(d.sqr() - c.r.sqr())) / d;
res.push_back(line{x, (c.c-x).rescale(c1) + (c.c-x).Rrot().rescale(c2)});
res.push_back(line{x, (c.c-x).rescale(c1) + (c.c-x).Lrot().rescale(c2)});
}
return res;
}
|